Question

ktioner för Quiz Fråga 1 20 po On a television program, a comedian tosses a watermelon from the top of a five-story building. The height of the watermelon as it falls is given by the function h(t) = -16t2 + 16+ + 60 where is the number of seconds since the watermelon was tossed. The quadratic expression in the function can be factored as h(t) = -4 ( 2t + 3) (2t - 5) How many seconds does the watermelon fall before it hits the ground

Answer 1

`h(t)=-16t^2+16t+60`

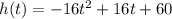
where h(t) is the height of the watermelon, and t is time in seconds

The function can also be expressed as :

`h(t)=-4(2t+3)(2t-5)`

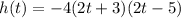
when the watermelon hits the ground, h(t) = 0, then:

`\begin{gathered} 0=-4(2t+3)(2t-5) \\ 0=(2t+3)(2t-5) \end{gathered}`

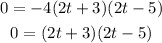
we have two options:

`\begin{gathered} 2t+3=0 \\ 2t=-3 \\ t=-(3)/(2) \end{gathered}`

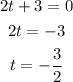
or

`\begin{gathered} 2t-5=0 \\ 2t=5 \\ t=(5)/(2) \\ t=2.5 \end{gathered}`

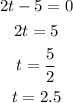
The negative solution has no sense in the context of this problem, then the watermelon takes 2.5 seconds to hit the ground