Question

The function gives the cost to manufacture x items.C(x) = 10,000 + 70x + 1100/XLevel of production x= 100Find the average cost per unit of manufacturing h more items (i.e., the average rate of change of the total cost) at a production level of x, where x is as indicated and h = 10 and 1. (Use smaller values of h to check your estimates.) HINT (See Example 1.] (Round your answers to two decimal places.) h 10 1 Cave 70.1 x 7.01 X Estimate the instantaneous rate of change of the total cost at the given production level x, specifying the units of measurement. C'(100) = 69.89 $/item

Answer 1

We have to calculate the average cost per unit of manufacturing h more items.

We first calculate the total additional cost:

`\begin{gathered} C(x+h)-C(x) \\ 10000+70(x+h)+(1100)/(x+h)-(10000+70x+(1100)/(x)) \\ (10000-10000+70(x+h-x)+(1100)/(x+h)-(1100)/(x)) \\ 0+70h+1100((x-(x+h))/(x(x+h))) \\ 70h+1100((h)/(x^2+h)) \end{gathered}`

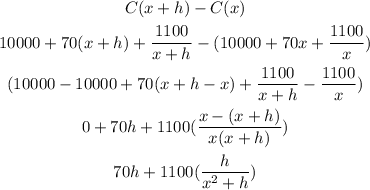
To calculate the average cost, we divide the total additional cost by the number of additional units h:

`\begin{gathered} C_(av)=(C(x+h)-C(x))/(h) \\ C_(av)=(70h+1100((h)/(x^2+h)))/(h)=70+1100((1)/(x^2+h)) \end{gathered}`

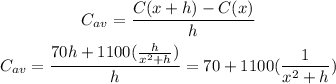
If the level of production is x=100, we can write:

`C_(av)=70+1100((1)/(100^2+h))=70+1100((1)/(10000+h))`

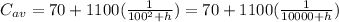
Then, for h=10 we have:

`C_(av)=70+1100((1)/(10000+10))=70+(1100)/(10010)=70+0.10989=70.10989`

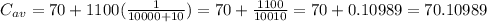
When h=1, we have:

`C_(av)=70+1100((1)/(10000+1))=70+(1100)/(10001)=70+0.10999=70.10999`

When h tends to 0, we can calculate:

`C_(av)=70+1100((1)/(10000+0))=70+0.11=70.11`

Answer:

The average unit cost of h=10 more units is 70.10989.

When h=1, the average unit cost is 70.10999.

The average unit cost of an additional unit, at the level of production x=100 (also known as "marginal unit cost" C'(x)) is 70.11.