Question

Calculus early transcendental functions. I need help seeing how to solve

Answer 1

The Solution:

Given the logarithmic equation below:

`\log _2x+\log _2(x+1)=\log _2(x-1)+\log _26`

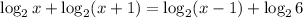
We are required to find the value(s) of x.

`\begin{gathered} \log _2x+\log _2(x+1)=\log _2(x-1)+\log _26 \\ \text{ Applying the product rule of logarithmic theory to the equation above, we get} \\ \log _2x(x+1)=\log _26(x-1) \end{gathered}`

Dividing both sides by log to base 2, we have

`\begin{gathered} (\log _2)/(\log _2)x(x+1)=(\log _2)/(\log _2)6(x-1) \\ \\ x(x+1)=6(x-1) \end{gathered}`

Clearing the brackets, we get

`\begin{gathered} x^2+x=6x-6 \\ \text{Collecting the like terms, we get} \\ x^2+x-6x+6=0 \\ x^2-5x+6=0 \end{gathered}`

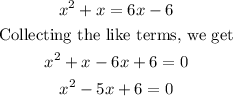
Solving the above quadratic equation using the Factorization Method, we get

`\begin{gathered} x^2-2x-3x+6=0 \\ x(x-2)-3(x-2)=0 \\ (x-3)(x-2)=0_{}_{} \\ x-3=0\text{ or x-2=0} \\ x=3\text{ or x=2} \end{gathered}`

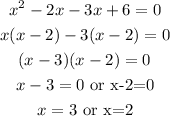
Therefore, the correct answer are: x=3 or x=2