Question

Mr. Jones owns 4 pairs of pants, 7 shirts, and 3 sweaters. In how many ways can he choose 2 pairs of pants, 3 shirts, and 1 sweater for a trip?

Answer 1

Given that Mr. Jones owns 4 pairs of pants, 7 shirts, and 3 sweaters. We are asked to find the number of ways he can choose 2 pairs of pants, 3 shirts, and 1 sweater for a trip.

Step-by-step explanation

The question above is a case of selection that refers to Combination. We will be using the formula below.

`^nC_r=(n!)/((n-r)!r!)`

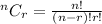
Therefore, we will apply the above formula to solve the question.

`^4C_2*^7C_3*^3C_1`

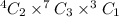
This implies that there are C(4,2) = 6 ways to choose 2 pairs of pants. There are C(7,3) = 35 ways to choose 3 shirts. There are C(3,1) = 3 ways to choose a sweater. So in total, there are

`\begin{gathered} =(4!)/(2!2!)*(7!)/(3!4!)*(3!)/(1!2!) \\ =6*35*3=630 \end{gathered}`

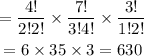
Answer: 630 ways