Question

Which ordered pair is included in the solution set to the following system?y < x^2 + 3y > x^2 – 2x + 8(–4, 2)(0, 6)(1, 12)(4, 18)

Answer 1

`\begin{gathered} yx^2-2x+8 \end{gathered}`

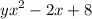
To determine which of the 4 pairs is part of the solution set, let's simply replace the value of "x" in the inequalities above and see if it makes the expression true or not.

Let's start with (-4, 2). Replace "x" with -4 and "y" with 2. Let's use the first inequality.

Since it is false for the second inequality, (-4, 2) is not part of the solution set.

Let's move on to (0, 6). Replace "x" with 0 and "y" with 6.

[tex]\begin{gathered} yOnce again, (1, 12) is false for the first inequality. Hence, (1,12) is not part of the solution set.

Lastly, let's check the 4th pair (4, 18). Replace "x" with 4 and "y" with 18.

[tex]\begin{gathered} yLet's also check if it is true for the second inequality,[tex]\begin{gathered} y>x^2-2x+8 \\ 18>4^2-2(4)+8 \\ 18>16-8+8 \\ 18>16-TRUE \end{gathered}" src="

As we can see above, the ordered pair (4, 18) makes both inequalities true hence, (4, 18) is included in the solution set of the given system of inequalities. (Option 4)