Question

When looking at a rational function, Jamal and Angie have two different thoughts. Jamal says that the function is defined at x = -3, x = -4, and x = 6. Angie says that the function is undefined at those x values. Describe a situation where Jamal is correct, and describe a situation where Angie is correct. Is it possible for a situation to exist that they are both correct? Justify your reasoning.

Answer 1

Answer: Hello!

a rational function is undefined when has a denominator equal to zero, if we have the points x = -3, x = -4 and x= 6, Angie is right when the function has the form of
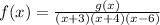`f(x) = (g(x))/((x +3)(x+4)(x-6))` where g(x) is a function defined in all the domain.

Then Jamal is correct when f(x) = g(x)/a(x) (because we already know that g(x) is defined in all the domain) where a(x) is not 0 in the points x = -3, x= -4 and x= 6 (for example take a(x) = 3x, that is only 0 when x =0).

there can't be a case where a function is undefined and defined at one point, then both of them can't be correct.

You could think in the next function:

`f(x) = (x^(2)-9 )/(x+3)`

in this case, when x = -3 both denominator and numerator are equal to zero, then you could think that this function is undefined at the point x= -3

but we can factorize the numerator as:

`f(x) = (x^(2) - 3^(2) )/(x + 3) = ((x+3)(x-3))/(x+3) = x-3`

then this function, that early looked like undefined at x = -3, is actually defined at that point.

Answer 2

rational function is a function that contains a fraction.

Jamal is correct if the numerator of the fraction contains the variable x and its denominator is an integer that is not 0.

Angie is correct if the denominator of the fraction contains the variable x and substituting the value of x will result to a denominator of 0.

A rational function can't be a function if its denominator is 0.