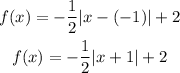Question

Write the equation of the function graphed in red below which is a transformation of the function f (x) = |x| (graphed in blue).

Answer 1

`f(x)=-(1)/(2)|x+1|+2`

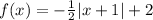
Step-by-step explanation:

Given the equation of the function graphed in blue, which is also the parent function;

`f(x)=|x|`

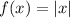
An equation of an absolute function after a transformation will be in the form;

`f(x)=a|x-h|+k`

when a > 0, the graph will open upwards

a < 0, the graph will open downwards

0 < a < 1, the graph will be compressed

a > 1, the graph will be stretched

h > 0, the graph will be translated h units to the right

h < 0, the graph will be translated h units to the left

k > 0, the graph will be translated k units upwards

k < 0, the graph will be translated k units downwards

Looking at the function graphed in red, we can notice the below;

*The graph opens downwards, this shows that a is negative.

*The graph moves 2 units upwards, this shows that k = 2

*The graph moves 1 unit to the left, this shows that h = -1

*The graph is compressed by a factor of 1/2, therefore a = 1/2

If we substitute these values into the equation above, we'll have;

`\begin{gathered} f(x)=-(1)/(2)|x-(-1)|+2 \\ f(x)=-(1)/(2)|x+1|+2 \end{gathered}`