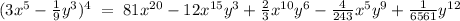Question

I need help with this practice problem *MAKE SURE TO ANSWER (a) AND (b), AS THEY ARE THE QUESTIONS TO THIS PROBLEM*

Answer 1

A)

Using the Binomial Theorem:

`(a+b)^n=\sum ^n_(k\mathop=0)\begin{pmatrix}n \\ k\end{pmatrix}a^(n-k)b^k`

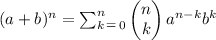
Then, replace for a=3x⁵, b=-1/9 y³ and n=4 to find the summation notation that Harold uses to express the expansion:

`\mleft(3x^5-(1)/(9)y^3\mright)^4=\displaystyle\sum ^4_(k=0)\begin{pmatrix}4 \\ k\end{pmatrix}\mleft(3x^5\mright)^(4-k)\mleft(-(1)/(9)y^3\mright)^k`

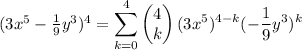
B)

To find the simplified terms of the expansion, expand the sum using the corresponding values of k from 0 to 4:

`\begin{aligned}\mleft(3x^5-(1)/(9)y^3\mright)^4\quad = & \quad \begin{pmatrix}4 \\ 0\end{pmatrix}(3x^5)^(4-0)(-(1)/(9)y^3)^0 \\ & +\begin{pmatrix}4 \\ 1\end{pmatrix}(3x^5)^(4-1)(-(1)/(9)y^3)^1 \\ & +\begin{pmatrix}4 \\ 2\end{pmatrix}(3x^5)^(4-2)(-(1)/(9)y^3)^2 \\ & +\begin{pmatrix}4 \\ 3\end{pmatrix}(3x^5)^(4-3)(-(1)/(9)y^3)^3 \\ & +\begin{pmatrix}4 \\ 4\end{pmatrix}(3x^5)^(4-4)(-(1)/(9)y^3)^4 \\ \end{aligned}`

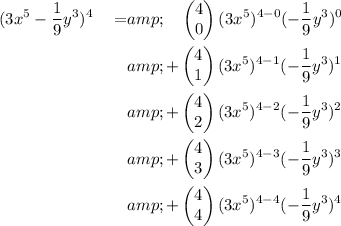
Simplify the exponents of the parentheses (3x^5):

`\begin{aligned}\mleft(3x^5-(1)/(9)y^3\mright)^4\quad = & \quad \begin{pmatrix}4 \\ 0\end{pmatrix}(3x^5)^4(-(1)/(9)y^3)^0 \\ & +\begin{pmatrix}4 \\ 1\end{pmatrix}(3x^5)^3(-(1)/(9)y^3)^1 \\ & +\begin{pmatrix}4 \\ 2\end{pmatrix}(3x^5)^2(-(1)/(9)y^3)^2 \\ & +\begin{pmatrix}4 \\ 3\end{pmatrix}(3x^5)^1(-(1)/(9)y^3)^3 \\ & +\begin{pmatrix}4 \\ 4\end{pmatrix}(3x^5)^0(-(1)/(9)y^3)^4 \\ \end{aligned}`

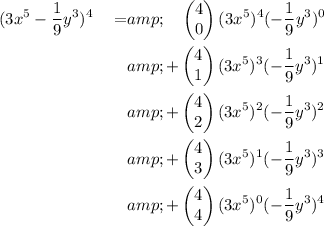
Simplify the binomial coefficients:

`\begin{aligned}\mleft(3x^5-(1)/(9)y^3\mright)^4\quad = & \quad 1\cdot(3x^5)^4(-(1)/(9)y^3)^0 \\ & +4\cdot(3x^5)^3(-(1)/(9)y^3)^1 \\ & +6\cdot(3x^5)^2(-(1)/(9)y^3)^2 \\ & +4\cdot(3x^5)^1(-(1)/(9)y^3)^3 \\ & +1\cdot(3x^5)^0(-(1)/(9)y^3)^4 \\ \end{aligned}`

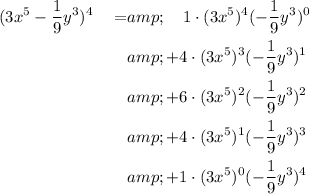
Elevate each parenthesis to its corresponding power:

`\begin{aligned}\mleft(3x^5-(1)/(9)y^3\mright)^4\quad = & \quad (81x^(20))(1) \\ & +4(27x^(15))(-(1)/(9)y^3) \\ & +6(9x^(10))((1)/(81)y^6) \\ & +4(3x^5)(-(1)/(729)y^9) \\ & +(1)((1)/(6561)y^(12)) \\ \end{aligned}`

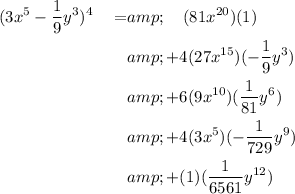
Next, multiply all the factors on each term:

`\begin{aligned}\mleft(3x^5-(1)/(9)y^3\mright)^4\quad = & \quad 81x^(20) \\ & -(108)/(9)x^(15)y^3 \\ & +(54)/(81)x^(10)y^6 \\ & -(12)/(729)x^5y^9 \\ & +(1)/(6561)y^(12) \\ \end{aligned}`

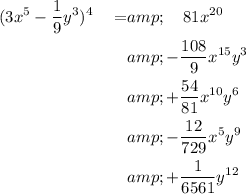
Finally, simplify all the coefficients:

`\begin{aligned}\mleft(3x^5-(1)/(9)y^3\mright)^4\quad = & \quad 81x^(20) \\ & -12x^(15)y^3 \\ & +(2)/(3)x^(10)y^6 \\ & -(4)/(243)x^5y^9 \\ & +(1)/(6561)y^(12) \\ \end{aligned}`

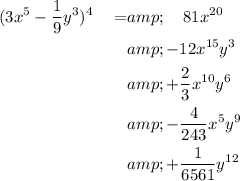
Therefore, the simplified terms of the expansion are:

`\mleft(3x^5-(1)/(9)y^3\mright)^4\; =\; 81x^(20)-12x^(15)y^3+(2)/(3)x^(10)y^6-(4)/(243)x^5y^9+(1)/(6561)y^(12)`