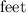Question

the area of a rectangular wall of barn is 160 square feet. its length is 4 feet longer than twice its width. find the width of the wall of the barn

Answer 1

The solution for finding the width of the wall of the barn is as follows:

W + 4 equals length.

Multiply width time length to equal 160.

W(w+4) = 160

w(squared) + 4w equals 160.

W = 10.80 ft

Therefore, the width of the wall of the barn is 10.80 ft

I hope that helps you.

Answer 2

8 feet

Explanation:

Given: the area of a rectangular wall of barn is 160 square feet. its length is 4 feet longer than twice its width.

To Find: the width of the wall of the barn

Solution:

Area of rectangular wall of barn
`=160`
`\text{sq.feet}`

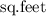
Let the length of wall of barn is
`=\text{l}`

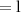
Let the width of wall of barn is
`=\text{b}`

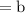
now,

length of wall of barn is,
`\text{l}=2\text{b}+4`

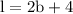
Area of wall of barn
`=\text{length}*\text{width}`

`=\text{l}*\text{b}`

`(2\text{b}+4)\text{b}`

`(2\text{b}+4)\text{b}=160`

`2\text{b}^2+4\text{b}=160`

`\text{b}^2+2\text{b}=80`

`\text{b}^2+2\text{b}-80=0`

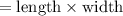
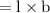
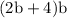
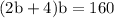
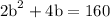
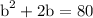
on factorizing

`(\text{b}+10)(\text{b}-8)=0`

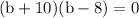
as width cannot be less than zero,

`\text{b}=8`
`\text{feet}`

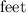
Width of the wall of barn is
`8`
`\text{feet}`