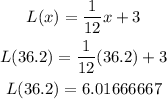Question

Use linear approximation, i.e. the tangent line, to approximate sqrt(36.2) as follows Let f(x) = sqrt(x) Find the equation of the tangent line to f(x) at x = 36

Answer 1

Answer: 6.01666667

Step-by-step explanation:

The slope of the line tangent to f(x)=√x is the derivative of the function which is:

`f^(\prime)(x)=(1)/(2√(x))`

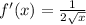
This means that at x=36, the slope is:

`\begin{gathered} f^(\prime)(x)=(1)/(2√(x)) \\ f^(\prime)(36)=(1)/(2√(36))=(1)/(12) \end{gathered}`

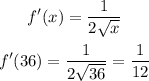
The function value for x=36 is:

`\begin{gathered} f(x)=√(x) \\ f(36)=√(36)=6 \end{gathered}`

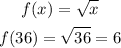
This means that the point on the curve we are being asked to find the equation of the tangent line would be (36, 6). Using the point-slope form:

`\begin{gathered} y-6=(1)/(12)(x-36) \\ y-6=(1)/(12)x-3 \\ y=(1)/(12)x-3+6 \\ y=(1)/(12)x+3 \\ L(x)=(1)/(12)x+3 \end{gathered}`

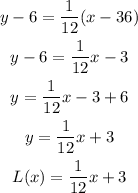
With this, the linear approximation of √36.2 would be:

`\begin{gathered} L(x)=(1)/(12)x+3 \\ L(36.2)=(1)/(12)(36.2)+3 \\ L(36.2)=6.01666667 \end{gathered}`