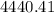First, divide the annual interest by 2 to find the semmiannual rate:

Each six months period, the current amount of money in the account gets a 1.05% increase. There are 10 periods of 6 months in a time interval of 5 years. Then, the 1.05% increase is appliead 10 times over the $4000 initial deposit.
To apply an increase of 1.05% is the same as multiplying the initial amount by a factor of:
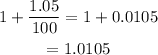
To apply that increase 10 times is the same as multiplying the initial amount by a factor of 1.0105 10 times, which is the same as multiplying the initial amount by a factor of:
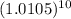
Then, the amount of money that she will have in the account after 5 years, is:

Therefore, the amount of money in the account after 5 years to the nearest cent, is: