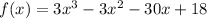Question

Construct a polynomial function with the following properties: third degree, 2 is a zero of multiplicity 2, -3 is the only other zero, leading coefficient is 3.

Answer 1

Data:

f(x) = 0 in x = 2; x = 2; x = - 3

Using the zeros we can form the function as follow:

A zero is the point where the function is 0, if a zero is 2 it means that in x=2 f(x)=0. we can express that like:

`f(2)=0`

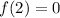
and then we can know that it is zero if :

`(x-2)=0`

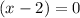
because:

`f(x)=(x-2)\text{ }\Rightarrow f(2)=(2-2)=0`

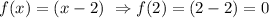
So using the zeros we form the equations as followç:

`f(x)=(x-2)(x-2)(x+3)`
`f(x)=(x^2-4x+2)(x+3)`
`f(x)=x^3+3x^2-4x^2-12x+2x+6=x^3-x^2-10x+6`

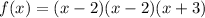
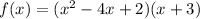
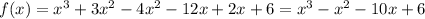
If we know that the leading coefficient is 3 then:

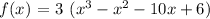`f(x)\text{ = 3 (}x^3-x^2-10x+6)`the final equation is:
`f(x)=3x^3-3x^2-30x+18`