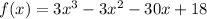Data:
f(x) = 0 in x = 2; x = 2; x = - 3
Using the zeros we can form the function as follow:
A zero is the point where the function is 0, if a zero is 2 it means that in x=2 f(x)=0. we can express that like:
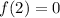
and then we can know that it is zero if :

because:
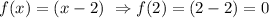
So using the zeros we form the equations as followç:
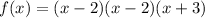
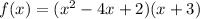

If we know that the leading coefficient is 3 then:
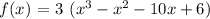 the final equation is:
the final equation is: