Solution
- The expression given is:
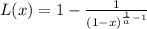
Question A:
- The question asks us to find the values of a such that L(x) is a rational function.
- To solve this question, we will rewrite the function by getting a common denominator, as follows:

- (This result answers Question B)
- Now that we have L(x) in this manner, we can infer that:
Since L(x) is a rational function, then, it means that the exponent on (1-x) must be a positive integer. Thus, let us assume this positive integer is n. Therefore, we can say:
![\begin{gathered} (1)/(a)-1=n \\ \text{Add 1 to both sides} \\ (1)/(a)=n+1 \\ \text{Invert both sides} \\ \therefore a=(1)/(n+1) \\ \\ \text{But we know that n is a positive integer} \\ \text{When n = }1 \\ a=(1)/(1+1)=(1)/(2) \\ \\ \text{When n = 2} \\ a=(1)/(1+2)=(1)/(3) \\ \\ \text{When n = 3} \\ a=(1)/(1+3)=(1)/(4) \\ \\ \text{Thus, we can observe that the values of }a\text{ that make the function }L(x)\text{ a rational function must be:} \\ a=(1)/(2),(1)/(3),(1)/(4),\ldots \end{gathered}]()
Question B:
The question would like us to express L(x) as a rational function. We have already done this process in Question A. We can simply repeat the process here:
![\begin{gathered} L(x)=1-\frac{1}{(1-x)^{(1)/(a)-1}} \\ \\ \text{Multiply numerator and denominator by }(1-x)^{(1)/(a)-1} \\ \\ L(x)=(1-\frac{1}{(1-x)^{(1)/(a)-1}})*\frac{(1-x)^{(1)/(a)-1}}{(1-x)^{(1)/(a)-1}} \\ \\ L(x)=\frac{(1-x)^{(1)/(a)-1}}{(1-x)^{(1)/(a)-1}}-\frac{(1-x)^{(1)/(a)-1}}{((1-x)^{(1)/(a)-1})^2} \\ \\ L(x)=\frac{(1-x)^{(1)/(a)-1}}{(1-x)^{(1)/(a)-1}}-\frac{1}{(1-x)^{(1)/(a)-1}} \\ \\ \text{The expression now has a common denominator, thus, we can combine both terms:} \\ \\ L(x)=\frac{(1-x)^{(1)/(a)-1}-1}{(1-x)^{(1)/(a)-1}} \end{gathered}]()
Question C:
The end behavior of a graph is the value L(x) as x tends to infinity.
- However, we do not know the value of "a". Because of this, the end value of the function can approach negative or positive infinity as x tends to negative or positive infinity. A third scenario arises when a = 1. This makes the function tend to zero. But a cannot be 1 because of the constraint that the function L(x) must be a rational function.
- The 2 scenarios described are explained further below:
![\begin{gathered} \text{Scenario 1:} \\ \text{When }x\to\infty\text{ and }0<p></p><p>- Thus, the end-behavior of the graph is:</p>[tex]\begin{gathered} x\to\infty,L(x)\to1 \\ x\to-\infty,L(x)\to1 \end{gathered}]()