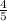General category: Mathematics
Sub-category: Improper fractions
Topic: Mixed number
Introduction:
A mixed number is a whole number plus a fractional part. On the other hand, an improper fraction is a fraction where the numerator is larger than the denominator.
Step-by-step explanation:
We have an equilateral triangle that has a perimeter of
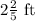
Notice that this number is a mixed number. To convert this mixed number to an improper fraction, we can perform the following steps:
Step 1: multiply the denominator by the whole number
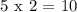
Step 2: add the answer from Step 1 to the numerator
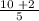
Step 3: write the answer from Step 2 over the denominator
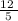
now, if the given triangle is an equilateral triangle, this means that the measure of each of its sides is the same. By definition, the perimeter of a polygon is the sum of its sides, thus if we denote by s any side of the equilateral triangle, we get the following equation:
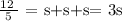
or
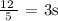
solving for s, we obtain:
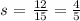
We can conclude that the correct answer is:
Answer:
The length of each side of the equilateral triangle is: