To graph the line that passes through the point (-6,-4) and has a slope equal to 2/3, the first step is to determine its equation.
To determine the equation of the line, use the point-slope form:
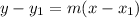
Where
(x₁,y₁) are the coordinates of one point of the line
m is the slope of the line
Replace the formula with the coordinates of the point x₁=-6 and y₁=-4, and the slope m=2/3
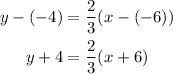
To be able to calculate two points of the line, let's write it in the slope-intercept form first:
-Distribute the multiplication on the parentheses term:
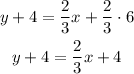
-Pass "+4" to the right side of the equation by applying the opposite operation "-4" to both sides of it:
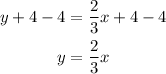
The next step is to choose two values of x and replace them in the formula to determine the coordinates for both additional points, I will use x=3 and x=-3
1) For x=3
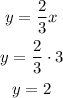
The coordinates are: (3,2)
2) For x=-3
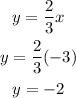
The coordinates are: (-3,-2)
Now you can graph the line, plot the coordinates of the three points (-6,-4), (-3,-2), and (3,2) in the coordinate system, then link them with a straight line: