Question

What is the simplest form of x^2+5x-6/x^2+9x+18?

A: x+2/x+6
B: 1/3
C:x-1/x+3
D:-1/3

Answer 1

the correct answer is c

Answer 2

C:
`(x-1)/(x+3)`

Explanation:

The simplest form of the expression below, can be found through factorization process.

`(x^(2)+5x-6)/(x^(2)+9x+18)`

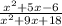
We have two quadratic expression. To find their factor, we only need to apply some steps:

Factorizing
`x^(2)+5x-6=(x+a)(x-b)`

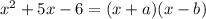
We have to find to numbers a and b that multiplied result in 6, but subtracted result in 5. We can see that
`a = 6` and
`b=1` are the right numbers, because 6 times 1 equals 6, and 6 minus 1 equals 5.

Therefore,
`x^(2)+5x-6=(x+6)(x-1)`

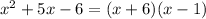
On the other expression, we applied the same process:

`x^(2)+9x+18=(x+6)(x+3)`; because,
`6(3)=18` and
`6+3=9`

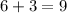
Then, we replace these factors for each expression:

`(x^(2)+5x-6)/(x^(2)+9x+18)`

`((x+6)(x-1))/((x+6)(x+3))`

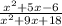
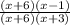
Eliminating similar factors, we have:

`((x-1))/((x+3))`

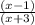
Which is the simples form.