Question

Complete the table and round to one decimal place as needed

Answer 1

We have been given the equation:

`A=P(1+(r)/(n))^(nt)`

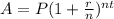
The table shows the values we need to input into the equation, we just need to identify them.

The amount invested is P.

The number of compounding periods is how many times the interest was compounded in one year, so it is n.

The annual interest is r.

The accumulated amount is A.

And the Times in years is t.

Since we have all the values but t, we need to first solve the equation for t:

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ (A)/(P)=(1+(r)/(n))^(nt) \\ \log _(10)((A)/(P))=\log _(10)((1+(r)/(n))^(nt)) \\ \log _(10)((A)/(P))=nt\log _(10)(1+(r)/(n)) \\ (\log_(10)((A)/(P)))/(n\log_(10)(1+(r)/(n)))=t \\ t=(\log_(10)((A)/(P)))/(n\log_(10)(1+(r)/(n))) \end{gathered}`

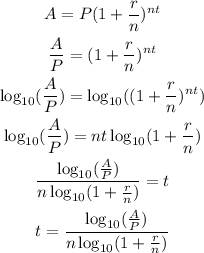
Now, we need to input the values.

The log we use can be any base, but they both have to be of the same base we chose. In this case, I used base 10.

So, inputting the values, we have:

So, the time t in years is approximately 8.7 years.