The given situation can be illustrated as follow:
In order to determine the minimum coefficient of static friction, it is necessary to find an expression for the friction force.
Due to the system is in equilibrium, the sum of all torques of the system around a certain pivot must be zero.
Then, if you consider the sum of torques around point B, you have:
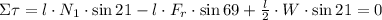
where l is the length of the ladder, W is the weight at the center of mass of the ladder, N1 is the normal force at the bottom of the ladder and Fr is the friction force. The signs of the terms of the previous equation indicate that torques rotate clockwise or counterclockwise.
By solving for Fr, you get:
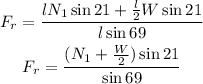
Now, consider that Fr = μ*N1, where μ is the coefficient of static friction. By replacing this expression of Fr into the last equation and by solving for μ you obtain:
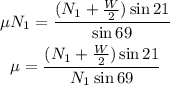
Moreover, consider that by the sum of forces in the vertical direction, you have:
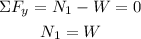
Then, you have for the coefficient of static friction:
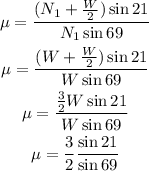
Hence, the coefficient of static friction between the ladder and the horizontal is:
