Question

The length of a rectangular piece of land is 90 yards more than three times its width. The perimeter is 780 yards . Find its dimensions.

Answer 1

Let's call X the length of the rectangular piece and Y the width of the rectangular piece.

First, the length of a rectangular piece of land is 90 yards more than three times its width. It means that we can write the following equation:

X = 90 + 3Y

Additionally, the perimeter is 780 yards, so we can write the equation:

2X + 2Y = 780

Therefore, replacing the first equation on the second equation and solving for Y, we get:

`\begin{gathered} 2X+2Y=780 \\ 2(90+3Y)+2Y=780 \\ 2\cdot90+2\cdot3Y+2Y=780 \\ 180+6Y+2Y=780 \\ 180+8Y=780 \\ 8Y=780-180 \\ 8Y=600 \\ Y=(600)/(8) \\ Y=75 \end{gathered}`

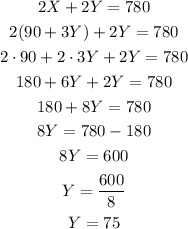
Now, we know that the width is equal to 75 yards, so we can calculated X as:

`\begin{gathered} X=90+3\cdot Y \\ X=90+3\cdot75 \\ X=315 \end{gathered}`

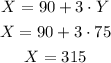
So, the length is 315 yards.

Answer: Length = 315 yards

Width = 75 yards