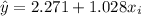Question

2.A linear model for the data in the table is shown in the scatter plot.(a)Which two points should you use to find the equation of the model? Circle the points on the graph.(b)What is the slope of the linear model? Show your work.(c)What is the equation of the linear model in point-slope form?(d)What is the slope-intercept form of the equation you wrote in Part (c)? Show your work.(e)What is the equation for the least squares regression line? Round the values for a and b to three decimal places. (Hint: Use a calculator or spreadsheet program.)

Answer 1

a) To find the equation of the model you have to use the points of the scatter plot that are closer to the line of best fit, these points are (6,9) and (10,13)

b) To determine the slope, you have to use the following formula:

`m=(y_2-y_1)/(x_2-x_1)`

Use the points (6,9) and (10,13)

`\begin{gathered} m=(13-9)/(10-6) \\ m=(4)/(4) \\ m=1 \end{gathered}`

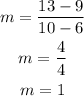
c) Use the calculated slope and one of the points to write the equation in the point-slope form:

`y-y_1=m(x-x_(1))_{}`

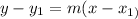
For m=1 and (6,9)

`\begin{gathered} y-9=1(x-6) \\ y-9=x-6 \end{gathered}`

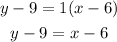
d) Add 9 to both sides of the expression to write the equation in the slope-intercept form.

`\begin{gathered} y-9+9=x-6+9 \\ y=x+3 \end{gathered}`

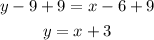
e) To determine the equation for the least square regression you have to use the following formulas:

`b=(\Sigma xy-(\Sigma x\cdot\Sigma y)/(n))/(\Sigma x^2-((\Sigma x)^2)/(n))`
`a=\bar{y}-b\bar{x}`

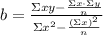
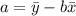
Calculate the sums of the values given on the table first:

`\begin{gathered} \Sigma x=1+2+5+6+7+9+10 \\ \Sigma x=40 \end{gathered}`
`\begin{gathered} \Sigma x^2=1^2+2^2+5^2+6^2+7^2+9^2+10^2 \\ \Sigma x^2=1+4+25+36+49+81+100 \\ \Sigma x^2=296 \end{gathered}`
`\begin{gathered} \bar{x}=(\Sigma x)/(n) \\ \bar{x}=(40)/(7) \end{gathered}`
`\begin{gathered} \Sigma y=2+6+6+9+11+10+13 \\ \Sigma y=57 \end{gathered}`
`\begin{gathered} \bar{y}=(\Sigma y)/(n) \\ \bar{y}=(57)/(7) \end{gathered}`
`\begin{gathered} \Sigma xy=1\cdot2+2\cdot6+5\cdot6+6\cdot9+7\cdot11+9\cdot10+10\cdot13 \\ \Sigma xy=2+12+30+54+77+90+130 \\ \Sigma xy=395 \end{gathered}`

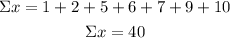
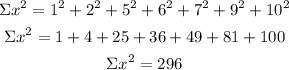
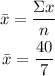
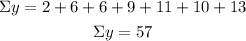
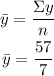
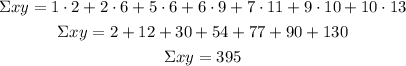
Calculate the slope of the linear regression (b)

`\begin{gathered} b=(395-(40\cdot57)/(7))/(296-(40^2)/(7)) \\ b=(395-(2280)/(7))/(296-(1600)/(7)) \\ b=(485)/(472)=1.0275\approx1.028 \end{gathered}`

Once you have obtained the slope, you can calculate the y-intercept (a)

`\begin{gathered} a=(57)/(7)-(485)/(472)\cdot(40)/(7) \\ a=(134)/(59)=2.271 \end{gathered}`

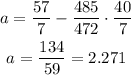
The equation of the regression model is:

`\hat{y}=2.271+1.028x_i`