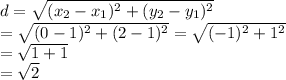The required line is parallel to line x + y = 1 and passes through point (1, 1).
For parallel lines, slope is equal.
x + y = 1
y = -x + 1 => slope is -1
Line passing though point (1, 1) with slope = -1 is given by y - 1 = -(x - 1)
y - 1 = -x + 1
y + x = 1 + 1 = 2
i.e. Equation of the required lin is x + y = 2
Required distance is the distance between point (1, 1) and the point of intersection of lines x + y = 2 and 2x - 3y = 4.
x + y = 2 . . . (1)
2x - 3y = 4 . . . (2)
(1) x 2 => 2x + 2y = 4 . . . (3)
(2) - (3) => -5y = 0 => y = 0
From (1), x + 0 = 2 => x = 2.
i.e. the point of intersection of lines x + y = 2 and 2x - 3y = 4 is (2, 0).
Required distance is