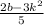Question

Solve for w k=2b-5w/3k

Answer 1

`k = (2b - 5w)/(3k)`

`3k^(2) = 2b - 5w`

`3k^(2) + 5w = 2b`

`5w = 2b - 3k^(2)`

`w = (2)/(5)b - (3)/(5)k^(2)`

Answer 2

b =
`(2b - 3k^(2) )/(5)`

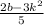
Explanation:

To solve for w in this equation;

k =
`(2b - 5w)/(3k)`

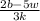
This implies we have to make w the subject of the formula.

To make w subject of the formula, first we cross multiply.

3k × k = 2b - 5w

3k² = 2b -5w

Now we will subtract 2b from both- side of the equation

3k² - 2b = -5w

we want to make the right hand side of the equation positive, to do that , we will just multiply through by minus sign. The equation becomes;

-3k² + 2b = 5w

We can rearrange the equation;

2b - 3k² = 5w

5w = 2b - 3k²

Then we will now divide both-side of the equation by 5

`(5w)/(5) = (2b - 3k^(2) )/(5)`

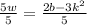
In the left side of the equation, the 5 at the numerator will cancel out the 5 at the denominator.

Hence;

w =
`(2b - 3k^(2) )/(5)`