Question

solve the given problem related to population growth.A city had a population of 22,500 in 2007 and a population of 24,800 in 2012.(a) Find the exponential growth function for the city. Use t=0 to represent 2007. Round k to five decimal places.N(t)=(b) Use the growth function to predict the population of the city in 2022. Round to the nearest hundred

Answer 1

`\begin{gathered} k=0.01946 \\ 30,126.81 \end{gathered}`

1) Since this is an exponential model, we need to write down the following exponential formula with the data provided by the question.

a) The exponential growth/decay is given by k like this this:

`\begin{gathered} y=ae^(kt) \\ 24800=22500e^(5k) \\ (24800)/(22500)=(22500)/(22500)e^(5k) \\ e^(5k)=(248)/(225) \\ \ln (1.92)=\ln e^(5k) \\ k=(\ln\left((248)/(225)\right))/(5) \\ k=0.01946 \end{gathered}`

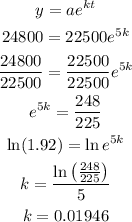
Note that the exponential growth is given by this formula, and now that found the value of k, we can predict with an approximate number the population of this city in 2022.

b) 2022 refers to 15 years later, so we can plug into t =15 and write down the following:

`\begin{gathered} N(t)=22500e^(15\cdot0.01946) \\ N(15)=22500e^(0.13047\cdot15) \\ N(15)=22500e^{\mleft\{0.2919\mright\}} \\ N(15)=30126.80506\ldots \\ N(15)\approx30,126.81 \end{gathered}`

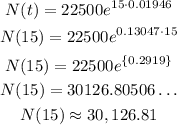
So, in 15 years the population is going to be something around 30127 people. (if we round to the nearest whole) Since the question wants to be in the decimal numbers for the nearest hundred, We can tell 30126.81