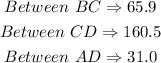Question

Given that the points A=(-1,4,0), B=(2,1,1), C=(2,-2,1), D=(-1,1,0) are four vertices of the parallelogram ABCD, determine the angles by using the dot product

Answer 1

GIVEN

The coordinates of the vertices of the parallelogram are given to be:

`A=\left(-1,4,0\right),B=\left(2,1,1\right),C=\left(2,-2,1\right),D=\left(-1,1,0\right)`

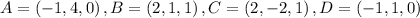
SOLUTION

Recall the formula used to calculate the angle between two vectors:

`\cos\theta=(A\cdot B)/(|A||B|)`

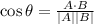
where A.B is the dot product of the vectors A and B.

The angle between vectors A and B can be calculated as follows:

`\begin{gathered} A=(-1,4,0) \\ B=(2,1,1) \\ \therefore \\ A\cdot B=(-1*2)+(4*1)+(0*1)=2 \\ |A|=√((-1)^2+4^2+0^2)=√(1+16)=√(17) \\ |B|=√(2^2+1^2+1^2)=√(4+1+1)=√(6) \end{gathered}`

Therefore:

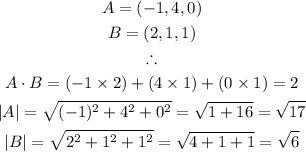
`\begin{gathered} \cos\theta=(2)/(√(17)√(6)) \\ \therefore \\ \theta=78.6\degree \end{gathered}`

The same pattern is followed for the other angles.

Hence, the angles are given to be:

`\begin{gathered} Between\text{ }BC\Rightarrow65.9\degree \\ Between\text{ }CD\Rightarrow160.5\degree \\ Between\text{ }AD\Rightarrow31.0\degree \end{gathered}`