Question

Let v(t)=t2−2tv(t)=t2−2t be the velocity, in feet per second, of an object at time tt, in seconds.

(a) What is the initial velocity?
(b) When does the object have a velocity of zero? If there is more than time, list all answers in a comma separated list.

Answer 1

Thee function is given as:

v(t)=t^2−2tv(t)=t^2−2t

(a) What is the initial velocity?

Base from the function, the initial velocity would be zero.

(b) When does the object have a velocity of zero?

It would be during time zero. Also, at a time equal to two.

Answer 2

v(0) =0

t=0,2

Explanation:

Given that velocity in feet per second of an object at time t in seconds is given by the quadratic equation

`v(t) = t^2-2t`

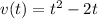
Initial velocity is the velocity at time 0.

Substitute t=0 in v(t)

a) Initial velocity =
`v(0) = 0^2-2(0)=0`

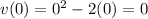
b) Equate velocity function to 0 and solve for t.

`v(t) = t^2-2t=0\\t(t-2)=0\\t=0,2`