1. The solution set is x (option B)
2. It is an identity (option B).
Let's solve the equation
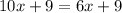 :
:
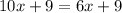
To solve this equation, we can start by isolating the variable terms:
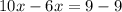
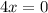
Dividing both sides by 4:
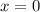
Now, let's determine the nature of the equation based on the solution we found.
The solution to the equation is
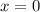 . This means that when you substitute
. This means that when you substitute
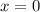 back into the original equation, it holds true:
back into the original equation, it holds true:
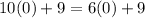
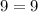
This equation is an identity because the solution
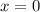 satisfies the equation for all values of
satisfies the equation for all values of
 .
.