Answer :
Let the final temperature be "T".
For the piece of copper :
- mass,
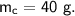
- specific heat capacity,
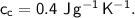
- initial temperature,
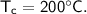
Then the heat of copper :
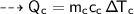
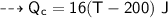
For copper calorimeter :
- mass,
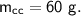
- specific heat capacity,
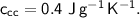
- initial temperature,
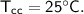
Then the heat of copper calorimeter :
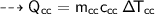

For water :
- mass,
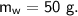
- specific heat capacity,
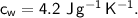
- initial temperature,
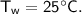
Then heat of water :

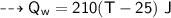
By energy conservation, the sum of all these energies should be zero as there were no heat energy change before the process, i.e.,
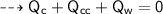
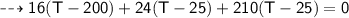
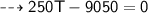
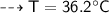

____________________________
[Note: in case of considering temperature difference it's not required to convert the temperatures from
 to K or K to
to K or K to
 .]
.]