Given:
The angle of incidence is
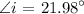
The light travels from the air to polystyrene.
The refractive index of air is n1 = 1
The refractive index of polystyrene is n2 = 1.6
Required: Angle of refracted ray.
Step-by-step explanation:
According to Snell's law,
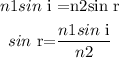
On substituting the values, the angle of refraction will be
![\begin{gathered} sin\text{ r =}\frac{1* sin\text{ 21.98}^(\circ)}{1.6} \\ r=sin^(-1)(\frac{1s\imaginaryI n(\text{21.98})^{\operatorname{\circ}}}{1.6}) \\ =13.53^(\circ) \end{gathered}]()
The angle of refraction is 13.53 degrees.
Final Answer: The angle of refraction is 13.53 degrees.