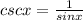Question

Did either student verify the identity property? Explain why or why not. Name 2 identities that were used in student A's verification and the steps they appear in.

Answer 1

The question is given below as

`cotx(cosx)=cscx-sinx`

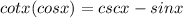
Step 1:

We will make use of the quotient identity below

`cotx=(cosx)/(sinx)`
`\begin{gathered} cotx(cosx)=cscx-s\imaginaryI nx \\ (cosx)/(sinx)(cosx)=cscx-s\mathrm{i}nx \\ (cos^2x)/(sinx)=cscx-s\mathrm{i}nx \end{gathered}`

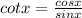
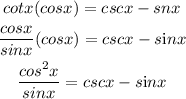
Step 2:

We will make use of the Pythagorean identity below

`\begin{gathered} cos^2x+sin^2x=1 \\ cos^2x=1-sin^2x \end{gathered}`
`\begin{gathered} (cos^(2)x)/(s\imaginaryI nx)=cscx-s\imaginaryI nx \\ (1-sin^2x)/(sinx)=cscx-s\mathrm{i}nx \\ (1)/(sinx)-(sin^2x)/(sinx)=cscx-s\mathrm{i}nx \\ cscx-sinx=cscx-s\mathrm{i}nx(PROVED) \end{gathered}`

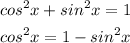
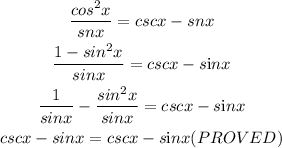
Hence,

STUDENT A and STUDENT B both proved it properly,

STUDENT A proved it from left to right

STUDENT B proved it from right to left

For STUDENT A's work,

Quotient identity was used in step 1

`cotx=(cosx)/(sinx)`

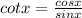
Pythagorean identity was used in step 3

`\begin{gathered} cos^2x+sin^2x=1 \\ cos^2x=1-sin^2x \end{gathered}`

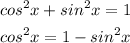
Reciprocal identity was used in step 5

`cscx=(1)/(sinx)`