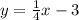Two lines are perpendicular if their slopes satisfy the following equation:
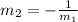
In this case, we have the line y = -4x - 6 which slope is m = -4, so the line perpendicular to this has a slope equal to:
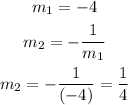
Also, we know the line we are looking for passes through the point (0, -3), so we can found the equation:

Above we found the value of the y-intercept value as -3, so the equation of the line is: