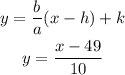Question

Write the equation for the hyperbola (below) in standard form and identify the vertices, foci and equations for the asymptotes. To earn full credit please share all steps and calculations. x^2+2x-100y^2-1000y+2401

Answer 1

Answer:
`((y+5)^2)/(7^2)-((x+1)^2)/(70^2)=1`
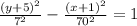
`\text{Foci = (}-1,\text{ -7}\sqrt[]{101}-5)\text{ and (}-1,\text{ -5+7}\sqrt[]{101})`

The vertex = (-1, -12) and (-1, 2)

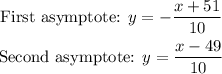
`\begin{gathered} \text{First asymptote: }y=-(x+51)/(10) \\ \text{Second asymptote: }y=(x-49)/(10) \end{gathered}`Step-by-step explanation:

The given equation of the hyperbola is:

`x^2+2x-100y^2-1000y+2401`

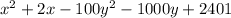
The standard form of the equation of a hyperbola is of the form

`(\mleft(y-k\mright)^2)/(b^2)-((x-h)^2)/(a^2)=1`

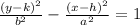
where (h, k) is the center of the hyperbola

The vertex = (h, k-b) and (h, k+b)

The given equation can be re-written as:

`\begin{gathered} x^2+2x-100(y^2+10y)+2401=0 \\ x^2+2x-100(y^2+10y)=-2401 \\ (x^2+2x+1)-100(y^2+10y+25)=-2401+1-25(100) \\ (x^2+2x+1)-100(y^2+10y+25)=-4900 \\ 100(y^2+10y+25)-(x^2+2x+1)=4900 \end{gathered}`

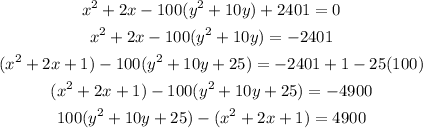
This can be further simplified into:

`\begin{gathered} 100(y+5)^2-(x+1)^2=4900 \\ \text{Divide through by 100} \\ (y+5)^2-((x+1)^2)/(100)=(4900)/(100) \\ (y+5)^2-((x+1)^2)/(100)=49 \\ ((y+5)^2)/(49)-((x+1)^2)/(4900)=1 \\ ((y+5)^2)/(7^2)-((x+1)^2)/(70^2)=1 \end{gathered}`

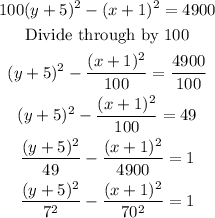
Therefore, the standard form of the given parabola equation is:

`((y+5)^2)/(7^2)-((x+1)^2)/(70^2)=1`

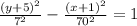
The center (h, k) = (-1, -5)

(a, b) = (70, 7)

The vertex = (-1, -5-7) and (-1, -5+7)

The vertex = (-1, -12) and (-1, 2)

The foci = (h, k-c) and (h, k+c)

`\begin{gathered} c=\sqrt[]{a^2+b^2} \\ c=\sqrt[]{70^2+7^2} \\ c=7\sqrt[]{101} \end{gathered}`
`\text{Foci = (}-1,\text{ -7}\sqrt[]{101}-5)\text{ and (}-1,\text{ -5+7}\sqrt[]{101})`

The first asymptote:

`\begin{gathered} y=-(b)/(a)(x-h)+k \\ y=-(x+51)/(10) \\ \end{gathered}`

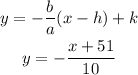
Second asymptote

`\begin{gathered} y=(b)/(a)(x-h)+k \\ y=(x-49)/(10) \end{gathered}`