Question

A) find a function that models the population t years after 2000 (t=0 for 2000). B) use the functions from part (a) to estimate the fox population in the year 2008.

Answer 1

the estimated fox population in the year 2008 is approximately 24,509 (rounded to the nearest integer).

To find a function that models the population \( t \) years after 2000 with an initial population of 14,000 and a continuous growth rate of 7% per year, we use the formula for continuous growth:

`\[ P(t) = P_0 \cdot e^(rt) \]`

where:

-
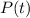`\( P(t) \)` is the population at time
`\( t \)`,

-
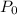`\( P_0 \)` is the initial population,

-
`\( r \)` is the growth rate,

-
`\( t \)` is the time in years since the start (year 2000 in this case),

-
`\( e \)` is the base of the natural logarithm.

Given:

-
`\( P_0 = 14000 \),`

-
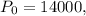
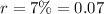`\( r = 7\% = 0.07 \)` (as a decimal),

-
`\( t = 8 \)`(for the year 2008, since \( 2008 - 2000 = 8 \)).

The function modeling the population is:

`\[ P(t) = 14000 \cdot e^(0.07t) \]`

To estimate the population in the year 2008, we substitute
`\( t = 8 \)` into the function:

`\[ P(8) = 14000 \cdot e^(0.07 \cdot 8) \]`

Calculating this gives us
`\( P(8) \approx 24509.42 \).`

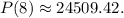
So, the estimated fox population in the year 2008 is approximately 24,509 (rounded to the nearest integer).

Answer 2

The Solution.

The function that models the population after t years is

`p(t)=ae^(bt)`

In this case,

`\begin{gathered} b=7\text{ \%=0.07} \\ \text{when t=0, p(0)=14000} \end{gathered}`

To find the value of a:

`14000=ae^((0.07*0))`
`\begin{gathered} 14000=a*1 \\ 14000=a \\ a=14000 \end{gathered}`

So, the required function is

`p(t)=14000e^(0.07t)`

To estimate the fox population in the year 2008, we have

`\begin{gathered} \text{ In this case, t=8 years} \\ p(t)=14000e^(0.07(8)) \\ p(t)=14000e^(0.56)=14000*1.7506725 \\ p(t)=24,509.415\approx24509 \end{gathered}`

Hence, the correct answer is 24509.