Question

Which of the following quadratic regression equations best fits the datashown below?X -4 -3 -2 -1 012 3 4y 56 30 15 34 820 44 60A. y = 5.02x² +3.66x + 4.16OB. y= 3.48x2 + 1.22x+3.44OC. y = 1.68x² + 1.06x + 4.96OD. y= 2.06x2 +0.18x+2.18

Answer 1

With the given data, we need to find the quadratic regression equation best fits. We can apply the least-square method.

The equation we have to find is in the form:

`y=ax^2+bx+c`

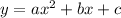
We need to find a, b and c.

So, let's start with the calculations:

Now, let's replace these sums into the following equations:

`\begin{gathered} a\sum_^x_i^4+b\sum_^x_i^3+c\sum_^x_i^2=\sum_^x_i^2y_i \\ a*708+b*0+c*60=2673\text{ Equation 1} \end{gathered}`
`\begin{gathered} a\sum_^x_i^3+b\sum_^x_i^2+c\sum_^x_i=\sum_^x_iy_i \\ a*0+b*60+c*0=73\text{ equation 2} \end{gathered}`
`\begin{gathered} a\sum_^x_i^2+b\sum_^x_i+c*n_i=\sum_^y_i \\ a*60+b*0+c*9=240\text{ Equation 3} \end{gathered}`

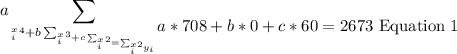
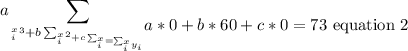
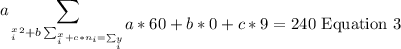
Now, let's solve for b in equation 2:

`\begin{gathered} 0+b*60+0=73 \\ b=(73)/(60) \\ b=1.22 \end{gathered}`

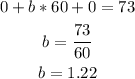
The next step is to isolate a from equation 3, and replace it into equation 1 to solve for c:

`\begin{gathered} 60a+9c=240 \\ 60a=240-9c \\ a=(240-9c)/(60) \\ a=4-(9)/(60)c \\ \\ \text{ Equation 1:} \\ 708a+60c=2673 \\ 708(4-(9)/(60)c)+60c=2673 \\ \\ 2832-(531)/(5)c+60c=2673 \\ \\ -(231)/(5)c=-159 \\ \\ c=(-159*5)/(-231) \\ \\ c=3.44 \end{gathered}`

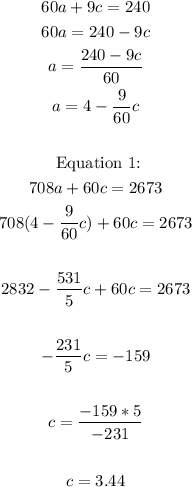
Finally, replace c into equation 3 and find a:

`\begin{gathered} 60a+9*3.44=240 \\ 60a=240-30.97 \\ 60a=209.03 \\ a=(209.03)/(60) \\ a=3.48 \end{gathered}`

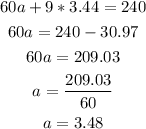
Finally, if we replace a, b and c into the quadratic regression equation we obtain:

`y=3.48x^2+1.22x+3.44`

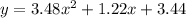
The answer is B.