Answer: a) A quadratic model for the data in the table:
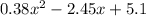 .
.
b) The population of bacteria at 9 hours will be 138,30
Step-by-step explanation:
a) General quadratic model formula :

By using data given we will have three quadratic equation:
(time:population):(x,y):(0, 5.1) , (1, 3.03) , (2, 1.72)
 ...(1)
...(1)
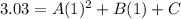 ...(2)
...(2)
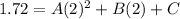 ....(3)
....(3)
On solving these equation we get value of constant A B and C:
A = 0.38 , B = -2.45 and C = 5.1
A quadratic model for the data in the table:
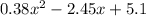
b) The population of bacteria at 9 hours
Using the Quadratic equation determined above:
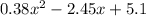
putting x = 9 hours
we get :
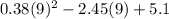 = 13.38
= 13.38
Since the data of population given is in thousands so the population of the bacteria at 9 hour will be 13,830.
The population of bacteria at 9 hours will be 138,30