Answer:
The solutions for the equation
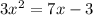 are:
are:
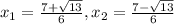 , so the option d is correct.
, so the option d is correct.
Explanation:
You have two options to find the solutions of the equation
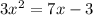
The first is to solve it with the quadratic formula, for this, you need to follow these steps:
- Add 3 and substract 7x from both sides
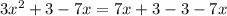
- Simplify

- Use the quadratic equation formula. For a quadratic equation of the form
 the solutions are
the solutions are
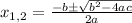
- In the equation given
 , so
, so

- The solutions are
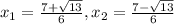
The second option is solve the equation by completing the square:
- Substract 7x from both sides
 and simplify
and simplify
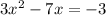
- Divide both sides by 3
 and simplify
and simplify

- Use the fact that

- We need to find
 , for this, we use this relation
, for this, we use this relation
 and solve for
and solve for
 , we get
, we get
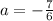
- Add
 to both sides in the equation of step 2
to both sides in the equation of step 2
 and simplify
and simplify
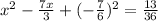
- Complete the square, use step 3,
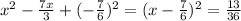
- For
 the solutions are
the solutions are
 , so
, so
