Question

If RT = 6 and RS = 9, then RX =

Answer 1

15 I think I hope this helps and if im wrong I'm soooooo sorry

Answer 2

RX=4

Explanation:

We are given:

RT = 6 and RS = 9

As RTS is a right angled triangle such that side RS is the hypotenuse of ΔRTS.

Hence on using the Pythagorean theorem we calculate the length of the side TS.

`RS^(2)=RT^2+TS^2\\\\9^2=6^2+TS^2\\\\81=36+TS^2\\\\TS^2=81-36=45\\\\TS=3√(5)`

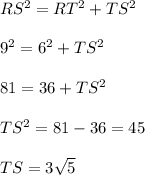
Now again in Right triangle TXS let the length of side SX be 'x'.

Now using Pythagorean Theorem in ΔTXS we have:

`TS^2=TX^2+SX^2\\\\45=TX^2+x^2\\\\TX^2=45-x^2`

As
`RX=RS-SX=9-x`

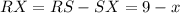
Now again using Pythagorean theorem in triangle TXR we have:

`RT^2=RX^2+TX^2\\\\6^2=(9-x)^2+(45-x^2)\\\\36=81+x^2-18x+45-x^2\\\\36=81-18x+45\\\\18x=81+45-36\\\\18x=90\\\\x=5`

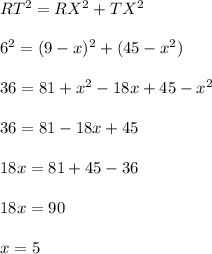
Hence, the length of side RX=9-5=4

RX=4