Answer:
4x+6 is the oblique asymptote.
Explanation:
we have to find the oblique asymptote for the given function :
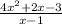
Oblique asymptote case arises when degree of numerator is greater than denominator
We divide the numerator by denominator to find the oblique asymptote.
You can see the long division in the attachement.
The quotient will give an equation which will be our required oblique asymptote.
4x+6 is the oblique asymptote.