Question

Which exponential function goes through the points (1, 16) and (4, 128)?

f(x) = 4(4)x

f(x) = 8(2)x

f(x) = 8(2)-x

f(x) = 4(4)-x

Answer 1

In this problem, we are given with the points (1, 16) and (4, 128) and is asked in the problem which among the functions correctly fits to the points. Via reverse engineering, we substitute the points to the functions and see which of them fits to the points. In this case, the answer to this problem is B. f(x) = 8 * 2^x

Answer 2

Option B is correct.

The exponential function goes through the points( 1, 16) and (4 , 128) is;
`f(x) = 8(2)^x`

Explanation:

The general form of the exponential function is given by;

`y=f(x) = ab^x` where a is the initial value and b is any value greater than 0.

If the exponential function goes through the points (1, 16) and (4, 128) we have;

`16 = ab^1`

16 = ab ......[1]

and

`128 = ab^4` .....[2]

Divide [2] by [1] we have;

`(128)/(16) =(ab^4)/(ab)`

Simplify:

`8 = b^3` or

`b^3 = 8`

Taking cube root both sides we get;

`b = \sqrt[3]{8} =\sqrt[3]{2^3}`

Simplify:

b = 2

Substitute the value of b = 2 in [1] we get;

`16 = a \cdot 2`

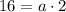
Divide both sides by 2 we get;

`(16)/(2) =(2a)/(2)`

Simplify:

a = 8

Substitute the value of a and b in
`f(x) = ab^x`

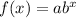
then we have;

`f(x) = 8(2)^x`

Therefore, the exponential function goes through the points( 1, 16) and (4 , 128) is;
`f(x) = 8(2)^x`