Question

Find the constant of variation for the quadratic variation.

9y = 4x2

A) -2
B) 4/9
C) 2/3
D) 9/4

Answer 1

option B is correct

The constant of variation is,
`k=(4)/(9)`.

Explanation:

Since the quadratic variation is the relationship between the variables x and y

i.e,
`y=kx^2`; where k is the quadratic variation.

Given quadratic equation:
`9y=4x^2` ...[1]

Division property of equality states that you divide the same number to both sides of an equation

Divide both side by 9,we get

`(9y)/(9)= (4)/(9)x^2`

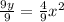
On simplifying we get;

`y= (4)/(9)x^2`

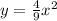
Now, compare above equation by equation[1] we get the value of k;

i.e,
`k=(4)/(9)`

Therefore, the constant of variation is,
`k=(4)/(9)`.

Answer 2

we are given the equation 9y = 4x2 and is asked in teh problem the constant of variation for the quadratic equation. In this case, the standard form is y = kx2 where k is the constant of variation. Hence we divide the equation by 9 such that k is equal to 4/9