Question

Use basic identities to simplify the expression. one divided by cotangent of theta to the second power. + sec θ cos θ

Answer 1

we are asked in the problem to simplify the expression one divided by cotangent of theta to the second power. + sec θ cos θ. the first term is expressed as tan2 θ. sec theta is the inverse of cos θ in which the second term is equal to 1. tan2 θ + 1 is equal to sec2 θ

Answer 2

The simplified expression is:

`(1)/(\cot^2 \theta)+\sec \theta\cos \theta=\sec^2 \theta`

Explanation:

We are asked to simplify the expression:

one divided by cotangent of theta to the second power+ sec θ cos θ

i.e. mathematically it is written as:

`=(1)/(\cot^2 \theta)+\sec \theta\cos \theta`

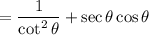
We know that:

`\tan \theta=(1)/(\cot \theta)\\\\i.e.\\\\(\tan \theta)^2=((1)/(\cot \theta))^2\\\\i.e.\\\\\tan^2 \theta=(1)/(\cot^2 \theta)`

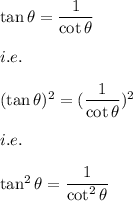
Hence, we can write this expression as:

`(1)/(\cot^2 \theta)+\sec \theta\cos \theta=\tan^2 \theta+\sec \theta\cos \theta`

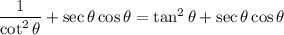
Also, we know that:

`\sec \theta=(1)/(\cos \theta)`

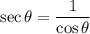
Hence, we have:

`\sec \theta\cos \theta=(\cos \theta)/(\cos \theta)\\\\\\i.e.\\\\\\\sec \theta\cos \theta=1`

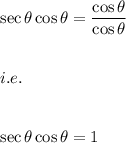
Hence, we get:

`=(1)/(\cot^2 \theta)+\sec \theta\cos \theta=\tan^2 \theta+1`

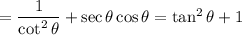
Also, we know that:

`\sec^2 \theta-\tan^2 \theta=1\\\\i.e.\\\\\sec^2 \theta=1+\tan^2 \theta`

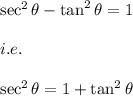
Hence, we get the simplified expression as:

`(1)/(\cot^2 \theta)+\sec \theta\cos \theta=\sec^2 \theta`