Question

A 1500 kg boat is traveling at 25 m/s. The captain stops giving the boat any gas, and the boatexperiences a frictional force of 906 N from the water over a distance of 115 m. What is thespeed of the boat after traveling this distance? Use the Law of Conservation of Energy tosolve.

Answer 1

We are given that a boat with an initial velocity of 25 m/s stops with a frictional force of 906 Newtons. We will analyze the energy of the boat at the beginning and after it has moved 115 meters.

At the beginning, the boat has kinetic energy. This kinetic energy is lost due to friction all the way until it has traveled the 115 meters. Therefore, the initial kinetic energy minus the energy lost due to friction must be equal to the final kinetic energy, we can write that like this:

`K_1-E_f=K_2`

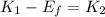
Where:

`\begin{gathered} K=\text{ kinetic energy} \\ E_f=\text{ energy lost due to friction} \end{gathered}`

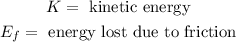
The kinetic energy is given by:

`K=(1)/(2)mv^2`

Where:

`\begin{gathered} m=\text{ mass} \\ v=\text{ velocity} \end{gathered}`

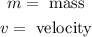
The energy lost due to friction is equal to:

`E_f=F_fd`

Where:

`\begin{gathered} F_f=\text{ frictional force} \\ d=\text{ distance} \end{gathered}`

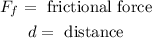
Substituting the equations we get:

`(1)/(2)mv^2_1-F_fd=(1)/(2)mv^2_2`

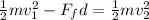
Now we solve for the final velocity. First, we multiply both sides by 2:

`mv^2_1-2F_fd=mv^2_2`

Now we divide both sides by the mass:

`v^2_1-(2F_fd)/(m)=v^2_2`

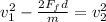
Now we take the square root to both sides:

`\sqrt{v^2_1-(2F_fd)/(m)}=v^{}_2`

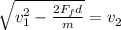
Now we substitute the values:

Solving the operations:

`22.05(m)/(s)=v_2`

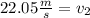
Therefore, the final velocity is 22.05 meters per second.