Answer:

Explanation:
The Factor Theorem tells us that substituting
 into a polynomial
into a polynomial
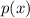 when divided by a linear factor
when divided by a linear factor
 will give us a value of 0 IF
will give us a value of 0 IF
 is a factor of the polynomial
is a factor of the polynomial
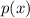
So, checking each of the 4 binomials, and getting a 0 as answer will tell us which one is a factor of the function given.
Putting
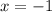 for
for
 into the function:
into the function:
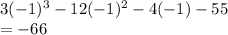
NOT a factor.
Putting
 for
for
 into the function:
into the function:
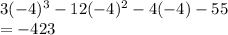
NOT a factor.
Putting
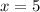 for
for
 into the function:
into the function:

IS a factor.
Putting
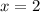 for
for
 into the function:
into the function:
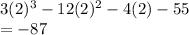
NOT a factor.
So we can see that only
 is a factor.
is a factor.