Answer:
Part 1) Infinite solutions
Part 2) No solutions
Part 3) Infinite solutions
Part 4) No solutions
Explanation:
Part 1) we have
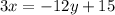
Group the variables
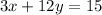 -------> equation A
-------> equation A
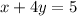 -------> equation B
-------> equation B
Multiply by
 equation B
equation B
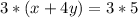 ------>
------>
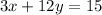
The equation A and the equation B are the same equation, is the same line
therefore
The system has infinite solutions
Part 2) we have
 -------> equation A
-------> equation A

Isolate the variable y
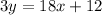 ------> Divide by
------> Divide by
 both sides
both sides
 -------> equation B
-------> equation B
we know that
If two lines has the same slope , then they are parallel lines
In this problem the line of the equation A and the line of the equation B has the same slope

therefore
Line A and Line B are parallel lines
The system has no solution
Part 3) we have
 -------> equation A
-------> equation A
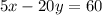 -------> equation B
-------> equation B
Multiply by
 equation A
equation A
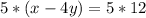 ------->
------->
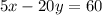
The equation A and the equation B are the same equation, is the same line
therefore
The system has infinite solutions
Part 4) we have
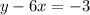
Isolate the variable y
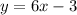 -------> equation A
-------> equation A
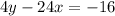
Isolate the variable y
 ------> Divide by
------> Divide by
 both sides
both sides
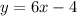 -------> equation B
-------> equation B
we know that
If two lines has the same slope , then they are parallel lines
In this problem the line of the equation A and the line of the equation B has the same slope

therefore
Line A and Line B are parallel lines
The system has no solution