Question

What is the value of log2 18 rounded to the nearest hundredth

Answer 1

Let x be the log to base 2 of 18. Then we can write:

`2^(x)=18`
Taking logs of both sides gives us:

`x\ log2=log18`

`x=(log18)/(log2)=4.17`
The answer is 4.17.

Answer 2

4.17

Explanation:

We have been given an expression
`\text{log}_2(18)`. We are asked to find the value of our given expression.

We can interpret our given expression as 2 raised to some power equals 18 and we need to find that power (x). We can represent our given information in an equation as:

`2^x=18`

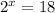
Upon taking natural log of both sides we will get,

`\text{ln}(2^x)=\text{ln}(18)`

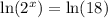
Using property
`\text{ln}(a^b)=b\cdot \text{ln}(a)` we will get,

`x\cdot \text{ln}(2)=\text{ln}(18)`

`\frac{x\cdot \text{ln}(2)}{\text{ln}(2)}=\frac{\text{ln}(18)}{\text{ln}(2)}`

`x=(2.8903717578961647)/(0.6931471805599453)`

`x=4.16992500144\approx 4.17`

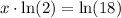
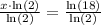
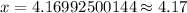
Therefore, the value of our given expression is 4.17.