The system of linear equations is,
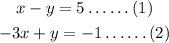
Consider the point (0,-1).
Check the first equation,
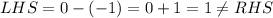
Since the point does not satisfy the equation (1), there is no need to check the other equation and it can be concluded that this point (0,-1) is not the point lying on both the lines.
Consider the point (3,8).
Check the first equation,
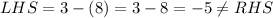
Since the point does not satisfy the equation (1), there is no need to check the other equation and it can be concluded that this point (0,-1) is not the point lying on both the lines.
Consider the point (-2,-7).
Check the first equation,
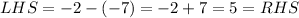
Check the second equation,
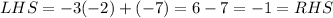
Here the point (-2,-7) satisfies both the equations. SO it can be concluded that the point is a common solution of the system of linear equations. Therefore, the point (-2,-7) will lie on both lines.
Consider the point (2,-3).
Check the first equation,
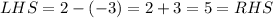
Check the second equation,
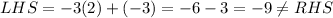
Since the point does not satisfy the equation (2), it can be concluded that this point (0,-1) is not the point lying on both the lines.