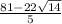this looks fun
ok so
we will use subsitution
xy=-10
divide both sides by x or y (I will choose y)
x=-10/y
sub -10/y fo x
(-10/y)^2+y^2=36
100/(y^2)+y^2=36
times both sides by y^2
100+y^4=36y^2
minus 36y^2 from both sides
y^4-36y^2+100=0
(y^2)^2-36(y^2)+100=0
quadratic formula
for
ax^2+bx+c=0
x=
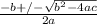
x=
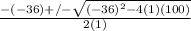
x=
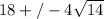
sub
y=-10/x
y=
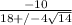
so x+y=
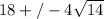
+
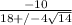
multiply first number by
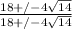
and add them
x+y=
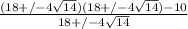
or
x+y=
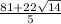
or