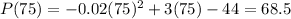A) For the first question, we will use the first and second derivative criteria. First, we will compute the first and second derivatives of the given function:
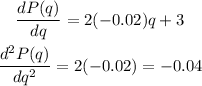
Now, we set the first derivative equals to zero and solve for q:
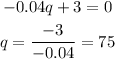
Evaluating q=75 in the second derivative, we get a negative value since it is a constant, therefore there is a maximum for q=75.
B) We know the maximum is reached for q=75 therefore to find the maximum profit we evaluate the function at q=75: