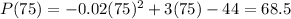Question

Suppose the Sunglasses Hut Company has a profit function given by P(q) = -0.02q2 + 3q - 44, where q is the number of thousands of pairs of sunglasses sold and produced, and P(q) is the total profit, in thousands of dollars, from selling and producing a pairs of sunglasses. A) How many pairs of sunglasses (in thousands) should be sold to maximize profits? (If necessary, round your answer to three decimal places.) Answer: thousand pairs of sunglasses need to be sold. B) What are the actual maximum profits (in thousands) that can be expected? (If necessary, round your answer to three decimal places.) Answer: thousand dollars of maximum profits can be expected.

Answer 1

A) For the first question, we will use the first and second derivative criteria. First, we will compute the first and second derivatives of the given function:

`\begin{gathered} (dP(q))/(dq)=2(-0.02)q+3 \\ (d^(2)P(q))/(dq^(2))=2(-0.02)=-0.04 \end{gathered}`

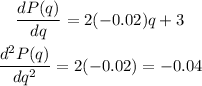
Now, we set the first derivative equals to zero and solve for q:

`\begin{gathered} -0.04q+3=0 \\ q=(-3)/(-0.04)=75 \end{gathered}`

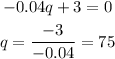
Evaluating q=75 in the second derivative, we get a negative value since it is a constant, therefore there is a maximum for q=75.

B) We know the maximum is reached for q=75 therefore to find the maximum profit we evaluate the function at q=75:

`P(75)=-0.02(75)^(2)+3(75)-44=68.5`