Question

a copper wire ( density = 8.96 g/cm^3 ) has a diameter of 0.25 mm. if a sample of this copper wire has a mass of 22 g, how long is the wire?

Answer 1

V = πr²H
r = 0,25mm / 2 = 0,125mm = 0,0125cm
d = 8,96 g/cm³
m = 22g


`d=(m)/(V)\\\\ \pi r^(2)H=(m)/(d)\\\\ H=(m)/(\pi r^(2)d)=(22g)/(\pi *(0,0125cm)^(2)*8,96(g)/(cm^(3)))=(22g)/(3,14*0,00015625cm^(2)8,96(g)/(cm^(3)))=\\\\\\\approx5004,55cm=50,0455m`

Answer 2

The length of the copper wire is 50.02 meters.

Step-by-step explanation:

It is given that,

Density of the copper wire,
`d=8.96\ g/cm^3=8960\ kg/m^3`

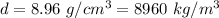
Diameter of copper wire, d = 0.25 mm = 0.00025 m

Radius of the copper wire, r = 0.000125 m

Mass of the copper, m = 22 g = 0.022 kg

We need to find the length of the wire. Let l is the length of the wire. The density of a copper wire is given by :

`d=(m)/(V)`

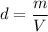
V is the volume of copper wire

`d=(m)/(\pi r^2h)`

`h=(m)/(d\pi r^2)`

`h=(0.022\ kg)/(8960\ kg/m^3* \pi (0.000125\ m)^2)`

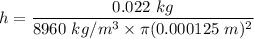
h = 50.02 m

So, the length of the wire is 50.02 meters. Hence, this is the required solution.